Was ist ein CIDR-Trie und wie kann er dir helfen?
In diesem Beitrag werden wir die CIDR-Trie-Datenstruktur erkunden und wie sie dir bei der Verwaltung von IP-Adressen und Subnetzen in deinem Rust-Projekt helfen kann.
Wie üblich in dieser Serie werden wir ein kleines Stück Rust aus einem realen Projekt nehmen und es auf eine sehr praktische Weise erklären.
Problem
Stell dir vor, dein Rust-Service soll nur von bestimmten IP-Adressen aus erreichbar sein. Dies kann wünschenswert sein, um den Zugriff auf bestimmte geografische Regionen zu beschränken (ähnlich wie Geo-Fencing) oder auf andere Dienste, die du kontrollierst.
Dieser Service sollte nicht durch die Notwendigkeit verlangsamt werden, die IP-Adresse jeder eingehenden Anfrage gegen eine Liste erlaubter IP-Adressen zu prüfen.
Schauen wir uns die Größe der geo-whois-asn-country-ipv4.csv-Datei an, die nur IPv4-Adressen enthält: Sie enthält 243K Einträge und ist etwa 7,13 MB groß. Jede eingehende Anfrage einfach mit Vec::contains gegen diese Liste zu prüfen, ist offensichtlich zu ineffizient.
Außerdem ist das Problem, dass wir nicht die Liste aller einzelnen IP-Adressen haben, die wir durchsuchen können, sondern wir haben eine Liste von IP-Bereichen, zum Beispiel:
- von
1.10.10.0bis1.10.10.255gehört zuIN/Indien - von
1.5.0.0bis1.5.255.255gehört zuJP/Japan
und so weiter.
Wenn sich nun ein Client mit unserem Service verbindet, müssen wir eine einzelne IP gegen diese gegebenen Bereiche prüfen und entscheiden, ob der Client sich verbinden darf oder nicht.
Lösung
Führen wir zunächst ein etwas anderes Format für diese IP-Bereiche ein, die CIDR-Notation. CIDR steht für Classless Inter-Domain Routing, und es ist eine kompakte Möglichkeit, einen IP-Adressbereich darzustellen. Zum Beispiel:
1.10.10.0bis1.10.10.255wird als1.10.10.0/24dargestellt1.5.0.0bis1.5.255.255wird als1.5.0.0/16dargestellt
Das Suffix /24 oder /16 sagt uns also, wie viele führende Bits der IP-Adresse fest sind. Bedenke, dass eine vollständige IPv4-Adresse 32 Bits hat. Das bedeutet, wenn 24 Bits fest sind, sind die verbleibenden 8 Bits variabel und, wie wir später sehen werden, für uns nicht wichtig.
Für diesen Beitrag nehmen wir an, dass wir bereits eine effiziente Möglichkeit haben, das obige Bereichsformat in die CIDR-Notation umzuwandeln. Wir wollen nun eine Datenstruktur finden, die gut geeignet ist, um nach dem Land einer gegebenen IP-Adresse zu suchen.
Letztendlich wollen wir die Datenstruktur in unserem Service so verwenden:
// Verwendungsbeispiel
let mut country_ip_list = CidrCountryMap::new();
country_ip_list.insert("1.10.10.0/24", "IN");
country_ip_list.insert("1.5.0.0/16", "JP");
// Suche nach dem Land der gegebenen IP-Adresse
assert_eq!(country_ip_list.search("1.10.10.1"), Some("IN"));
assert_eq!(country_ip_list.search("1.10.10.22"), Some("IN"));
assert_eq!(country_ip_list.search("1.5.0.1"), Some("JP"));
// nicht in der Liste
assert_eq!(country_ip_list.search("10.1.1.1"), None);
Hinweis: Dieser Code ist Pseudocode. In der Produktion würden wir wahrscheinlich keine Strings für die IP-Adressen verwenden, sondern den
std::net::Ipv4Addr-Typ der std lib.
Die CidrCountryMap
Eine Datenstruktur, auf der wir die CidrCountryMap basieren könnten, ist ein spezialisierter Trie. In seiner allgemeinsten Form kann er verwendet werden, um basierend auf dem Präfix eines Elements zu suchen (z.B. die ersten Buchstaben eines Strings).
Aber schauen wir uns zunächst an, was ein Trie ist und sein Anwendungsfall. Laut Wikipedia wird ein Trie auch digitaler Baum oder Präfixbaum genannt. Zitat:
Im Gegensatz zu einem binären Suchbaum speichern Knoten im Trie nicht ihren zugehörigen Schlüssel. Stattdessen definiert die Position eines Knotens im Trie den Schlüssel, mit dem er verknüpft ist. Dies verteilt den Wert jedes Schlüssels über die Datenstruktur und bedeutet, dass nicht jeder Knoten notwendigerweise einen zugehörigen Wert hat.
Der Kern ist also, dass wir keine vollständigen Werte auf Knoten speichern würden, sondern die Daten (die wir speichern wollen) sich auf mehrere Knoten im Baum auf einem Pfad verteilen. Ein Pfad, der an der Wurzel beginnt (normalerweise oben visualisiert) und hinunter zu einem Blatt (letzter Knoten im Baum) oder einem terminalen Knoten führt.
Diese Datenverteilung auf Pfaden bringt einige sehr nützliche Eigenschaften mit sich: Die Zeit, die es braucht, nach einem Element zu suchen, hängt nur von der Schlüssellänge ab, nicht von der Anzahl der gespeicherten Elemente. Das Gleiche gilt für das Einfügen von Elementen.
Die CIDR-Trie-Besonderheiten
Im CIDR-Trie repräsentieren wir ein Bit der IP-Adresse als einen Knoten auf dem Pfad. Der vollständige Pfad von der Wurzel zu einem (terminalen) Blattknoten repräsentiert daher die festen Bits der IP-Adresse (ohne die nachfolgenden maskierten Bits). Der Blattknoten speichert außerdem den Ländercode, der mit dem IP-Adressbereich verknüpft ist.
Schauen wir uns zum Beispiel den IP-Bereich 1.10.10.0/24 und ihre einzelnen Bytes an:
1 -> 00000001
10 -> 00001010
10 -> 00001010
0 -> 00000000
und das Suffix /24 sagt uns, dass die ersten 24 Bits diejenigen sind, die wir berücksichtigen. Das bedeutet, wir speichern die letzten 8 Bits des IP-Bereichs nicht.
Wir können also einen Trie bauen, genau wie wir diese Binärzahlen lesen würden, der so aussieht (zeigt nur die ersten 2 Bytes):
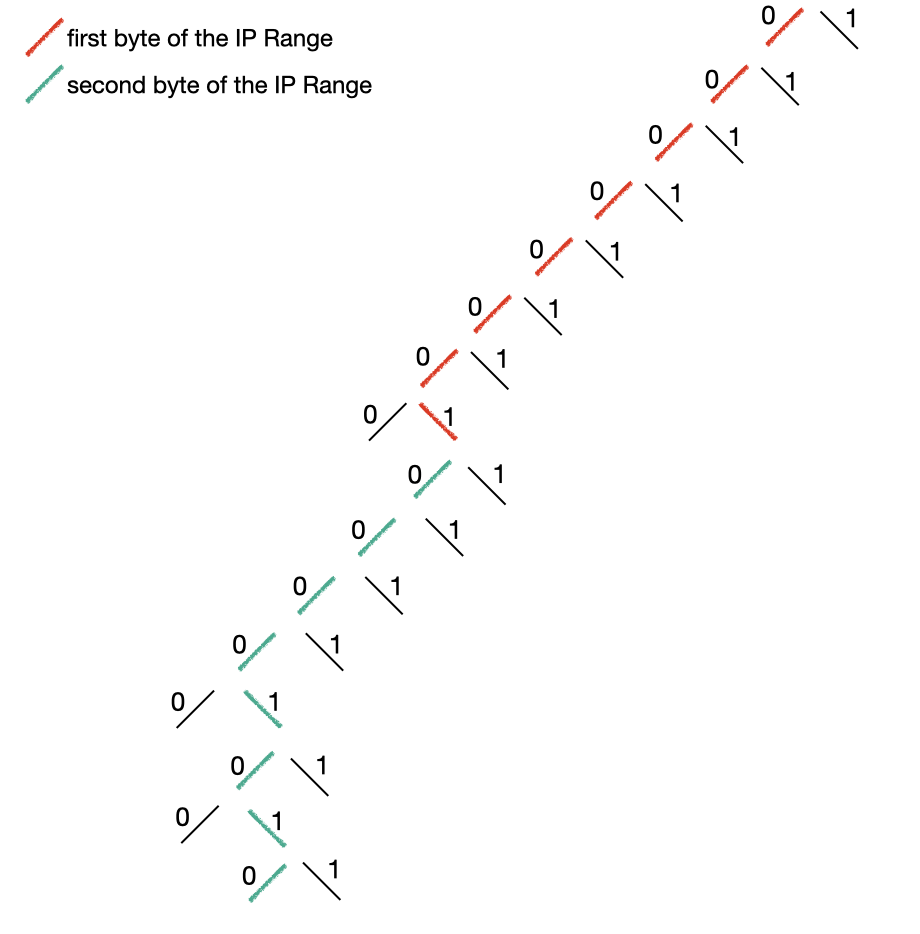
In der Illustration können wir den Pfad sehen, den die ersten 16 Bits der IP-Adresse überspannen würden. Die Knoten des 3. Bytes werden nicht gezeigt, um die Illustration einfach zu halten. Aber stell dir einfach einen fortgesetzten Pfad hinunter zum Blattknoten vor. Der Blattknoten würde den Ländercode enthalten und wäre auch als terminaler Knoten markiert.
Das bedeutet, wenn wir nach dem Land der IP-Adresse suchen wollen, müssen wir nur die Bits der gegebenen IP-Adresse verarbeiten und dem Pfad im Trie folgen. Wenn wir einen terminalen Knoten erreichen, haben wir den Ländercode gefunden.
Das ist die Grundidee des CIDR-Trie. Implementieren wir diesen Trie jetzt in Rust.
Implementierung
Führen wir das CidrCountryMap-Struct ein, das den Trie und die Methoden zum Einfügen und Suchen einer gegebenen IP-Adresse enthält.
#[derive(Default)]
pub struct CidrCountryMap {
root: Node,
}
Das Node-Struct repräsentiert einen einzelnen Knoten im Trie. Es enthält den Ländercode, die Kindknoten und behält die Information, ob es ein terminaler Knoten im gesamten Trie ist oder nicht.
#[derive(Default)]
struct Node {
is_terminal: bool,
children: [Option<Box<Node>>; 2],
value: Option<String>,
}
Hinweis: Wir verwenden ein Array fester Größe für 2 Nodes (
children: [Option<Box<Node>>;2]), um die Kindknoten darzustellen. Dies ist ein gängiges Muster in Rust, um eine Baumstruktur darzustellen. Dies vermeidet weitere Allokationen beim Einfügen von Knoten. Falls gewünscht, könnte man auch einenVecanstelle eines Arrays verwenden. Dies ist auch spezifisch für einen binären Trie, z.B. für das Speichern beliebiger ASCII-Zeichen müssten wir 256 Kinder (vor-)allokieren (eines pro Zeichen). In diesem Fall wäre es besser, eineHashMapanstelle eines Arrays fester Größe zu verwenden.
Wir müssen Box verwenden, weil Rust keine rekursiven Typen erlaubt, die nicht auf dem Heap liegen.
Implementieren wir die CidrCountryMap-Insert-Methode.
impl CidrCountryMap {
pub fn insert(&mut self, cidr: &str, data: impl Into<String>) -> Result<()> {
let (cidr, take_bits) = cidr
.split_once('/')
.ok_or(CidrCountryMapError::SplitError)?;
let mut take_bits = take_bits
.parse::<usize>()
.map_err(|err| CidrCountryMapError::ParseIntError(err))?;
let mut current_node = &mut self.root;
for byte in cidr.split('.').flat_map(|octet| octet.parse::<u8>()) {
for bi in (0..8).rev() {
if take_bits == 0 {
break;
}
let index = (byte >> bi) & 1;
current_node = current_node.children[index as usize].get_or_insert(Box::default());
take_bits -= 1;
}
}
current_node.is_terminal = true;
current_node.value = Some(data.into());
Ok(())
}}
- sie teilt die CIDR-Notation in die IP-Adresse und die Anzahl der Bits
- sie iteriert über die Bytes der IP-Adresse und die Bits der CIDR-Notation
- sie verarbeitet die Bits von links nach rechts durch Bit-Shifting und Maskierung
(byte >> bi) & 1(bi ist die Anzahl der Bits, die wir nach rechts verschieben)- zuerst verschieben wir um 7 Bits, dann um 6 Bits, dann um 5 Bits und so weiter
- nach dem Verschieben der Bits nach rechts wählen wir das rechteste Bit mit der Maske
1aus - dadurch iterieren wir durch die Bits des Bytes von links nach rechts
- dies ergibt entweder wahr oder falsch (1 oder 0) und wir verwenden dies als Index, um auf das Kind-Array zuzugreifen
- wir nehmen oder fügen einen neuen Knoten im Trie für jedes Bit ein
- am Ende ist
current_nodeder Blattknoten und wir setzen den Ländercode und markieren ihn als terminal
Hinweis: Du fragst dich vielleicht über die Verwendung von
Result<()>undCidrCountryMapError. Ich habe es absichtlich weggelassen, um den Code einfach zu halten und.unwrap()nicht zu verwenden. Den vollständigen Code findest du im Playground-Link im Referenzen-Abschnitt.
Die Such-Methode ist der Insert-Methode recht ähnlich. Wir müssen nur über die Bits der IP-Adresse iterieren und dem Pfad im Trie folgen.
impl CidrCountryMap {
pub fn search(&self, cidr: &str) -> Option<&str> {
let mut current_node = &self.root;
for byte in cidr.split('.').flat_map(|octet| octet.parse::<u8>()) {
for bi in (0..8).rev() {
let index = byte >> bi & 0b1;
if let Some(node) = ¤t_node.children[index as usize] {
current_node = node;
} else if current_node.is_terminal {
break;
} else {
return None;
}
}
}
current_node.value.as_deref()
}
}
- wir brechen die Schleife ab, wenn wir einen terminalen Knoten erreichen
- wir geben
Nonezurück, wenn wir einen Knoten erreichen, der keine Kinder hat - wir geben den Ländercode des Endknotens, des Blattknotens, zurück, wenn wir das Ende der IP-Adresse erreichen
Fazit
Die Suche einer IP-Adresse im CIDR-Trie wird in O(k) Zeitkomplexität durchgeführt. Wobei k die Anzahl der Bits in der nachzuschlagenden IP-Adresse ist, also O(32). Es kann auch weniger als O(k) Zeit dauern, wenn die IP nicht im Trie vorhanden ist.
Der CIDR-Trie ist eine sehr effiziente Datenstruktur, um nach IP-Adressen in einem gegebenen Bereich zu suchen.
Hinweis: Für andere komplexere Anwendungsfälle könnte es besser sein, die
trie_rs-Crate zu verwenden, die eine generischere Trie-Implementierung bietet. Ich möchte dich jedoch ermutigen, auf eine saubere und kleine Abhängigkeitsliste in deinen Projekten zu achten. Sei dir bewusst, dass jede externe Abhängigkeit mit den Kosten von Wartung und weniger Kontrolle über Sicherheit und Stabilität einhergeht.
Verbesserungsideen:
- wir könnten alle Trie-Knoten in einem einzelnen
Vecspeichern, um mehrere Allokationen zu vermeiden und die Cache-Lokalität zu verbessern - wir könnten den Trie komprimieren, indem wir Knoten kombinieren, die nur ein Kind haben, dieser Ansatz wird dann Radix-Trie genannt
- wir könnten den Ländercode in einem separaten Vektor speichern und den Index als Referenz in den Trie-Knoten verwenden, um Speicher zu sparen und zu vermeiden, den Ländercode mehrfach zu speichern
Besonderer Dank an Jonas und David für Feedback und Verbesserungsvorschläge zu diesem Beitrag